Berechnung schiefer Kegel

[xgx7]

Hallo!


An die Mathematiker unter euch:

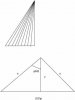
Vorgegeben sei ein schiefer Kreiskegel, wobei die Spitze genau oberhalb eines Punktes der Peripherie des Basiskreies liegt.

Wie berechnet man den Öffnungswinkel des abgewickelten Mantels des Kegels?


Gibt es dazu irgendwelche Links etc. ? Oder kann das hier jemand erklären?

Gruß xgx7

 

[Cortex85]

Spontan würde mir einfallen:
Berechne den Abstand zwischen der Spitze, dem Punkt auf der Peripherie des Basiskreises und dem Mittelpunkt des Basiskreises. Diese drei Punkte bilden ein Dreieck, von dem du ja die Kantenlängen berechnen kannst. Und mit Hilfe des Sinussatzes kannst du ja die Winkel in diesem Dreieck ausrechnen.

 

[KayHH]

Moin xgx7,

Oder kann das hier jemand erklären?

meinst du mit Öffnungswinkel den Winkel mit dem die Rotationsachse des Kegels auf die imaginäre Tischoberfläche stösst? Das wäre dann 90 Grad minus den halben Winkel in der Kegelspitze.

BTW, gibt es heute eigentlich noch Schulmathewettbewerbe auf Landes- und Bundesebene?


Gruss KayHH

 

[Squart]

In welcher Form hast du denn den Kreiskegel gegeben? Höhe? Radius des Kreises?

 

[KayHH]

Moin xgx7,

habe noch mal schnell einen Schnappschuß mit der DigiCam gemacht.


Gruss KayHH

 

[xgx7]

Erst einmal ein Danke für eure Antworten! :-D

Gegeben wären die Höhe des Kegels mit 7 cm und der Radius des Basiskreises mit 5 cm.

@KayHH

Nein, ich meine sozusagen den Winkel in der Spitze des Kegels, nur eben in der abgerollten Mantelfläche.

@Cortex85

Die Abstände berechnen ist ein leichtes, da ja die Spitze genau oberhalb eines Punktes der Peripherie des Basiskreises liegt. Der Abstand zwischen dem Punkt der Peripherie des Basiskreises und dem Mittelpunkt der Kreises ist damit der Radius des Kreises, und der Abstand zwischen Peripheriepunkt und Spitze die Höhe des Kegels.

PS: Ja, es gibt noch Mathe-Wettbewerbe. Die Besten des Kommunalen werden dann dahin eingeladen, bzw. IMHO zu den Wettbewerden auf Bundesebene die Besten der Landesebenen. Es gibt sogar Weltmeisterschaften!

 

[Squart]

[Andere Frage, auch zum Thema Mathematik]

Oh, da hätte ich auch eine Frage, vielleicht kann ich diese hier stellen (ein eigener Thread wäre übertrieben):
Gegeben ist eine konvergente Folge ak, welche gegen a konvergiert. Zu zeigen ist, dass das arithmetische Mittel dieser Folgenglieder auch gegen a konvergiert. Das ist der cauchysche Grenzwertsatz. Kennt irgendjemand einen guten Beweis oder zumindest eine Idee? (Konvergenz soll über epsilon-Umgebungen gezeigt werden)
http://de.wikipedia.org/wiki/Cauchyscher_Grenzwertsatz

Ich würde eigentlich so vorgehen, dass ich behaupten würde, dass der Grenzwert des arith. Mittels in jeder epsilon-Umgebung um a liegt. dazu würde ich die Behauptung aufstellen, dass endlich viele ak's ausreichen, so dass das arith. Mittel dieser ak's in einer epsilon-Umgebung um a liegt (unter diesen ak's sollen alle sein, die ausserhalb der epsilon-Umgebung sind).
Als weiteres würde ich zeigen, dass die restlichen ak's, die in der epsilon-Umgebung sind, auch nichts mehr daran ändern und jedes weitere arith. Mittel immer noch in der epsilon-Umgebung liegt.

Aber hoffentlich kennt ihr eine bessere Taktik, da ich einerseits nicht weiß, wie ich diese Behauptungen nachweisen soll und andererseits mir dies sehr umständlich vorkommt.

 

[tjp]

Re: [Andere Frage, auch zum Thema Mathematik]

Gegeben ist eine konvergente Folge ak, welche gegen a konvergiert. Zu zeigen ist, dass das arithmetische Mittel dieser Folgenglieder auch gegen a konvergiert. Das ist der cauchysche Grenzwertsatz. Kennt irgendjemand einen guten Beweis oder zumindest eine Idee?

Im Harro Heuser, Analysis I ist ein Beweis drin, morgen werfe ich mal ein Blick rein, heute abend habe ich kein Nerv mehr dazu.

 

[Cortex85]

Die Abstände berechnen ist ein leichtes, da ja die Spitze genau oberhalb eines Punktes der Peripherie des Basiskreises liegt. Der Abstand zwischen dem Punkt der Peripherie des Basiskreises und dem Mittelpunkt der Kreises ist damit der Radius des Kreises, und der Abstand zwischen Peripheriepunkt und Spitze die Höhe des Kegels.

Also hättest du schon ein (sogar rechtwinkliges) Dreieck, das von diesen drei Punkten (Spitze, Mittelpunk des Basiskreises und Peripheriepunkt unter der Spitze) gebildet wird. Dann musst du nur noch den Winkel zwischen den beiden Seiten des Dreiecks ausrechnen, die sich in der Spitze schneiden und mit 2 multiplizieren.
Eine andere Möglichkeit wäre:
Du stellt 2 Geradengleichungen auf:
1. Die Gerade Mittelpunkt des Basiskreises - Spitze
2. Peripheriepunkt - Spitze

und berechnest den Winkel dieser beiden, sich schneidenen Geraden mit der Formel:

cos(winkel) = Skalarprodukt der Richtungsvektoren / Summe der Beträge der Richtungsvektoren.

und multiplizierst dann den winkel mit 2.

@squart: Du könntest es mit vollständiger Induktion über die Glieder der Folge versuchen.

 

[KayHH]

Moin xgx7,

ich hoffe ich ahne was du meinst. Abgerollt gleich abgewickelt, spricht so als ob du den Kegel aus einem flachen Blatt Papier basteln möchtest?

2 x 5 x Pi = 31,51 Tatsächlicher Umfang als Kegel
2 x 7 x Pi = 44,12 Gesamtumfang als abgewickelter Kegel

Die Differenz (12,61) ergibt den äußeren Rand des fehlenden Segments. Das fehlende Segment verhält sich zum Gesamtumfang des flachen Kegels wie der gesuchte Winkel zu 360 Grad. Also 360 / (44,12 / 12,61) = 102,89 Grad. Dies ist der Winkel für das fehlende Segment. Der Rest ist dann eben 360 Grad minus diesem Wert.


Gruss KayHH


Nachtrag: Wenn das auch nicht die Frage war, mach doch mal 'ne Zeichnung.
Nachtrag 2: Ich sehe gerade „Höhe“. Das würde wohl bedeuten, dass die 7 cm oben nicht ganz richtig sind. Die Höhe an der Kegelaußenseite mit der du wirklich rechnen musst lässt sich mit Pythagoras aber leicht ausrechnen (7,43). Dann passt es.

 

[xgx7]

Also hättest du schon ein (sogar rechtwinkliges) Dreieck, das von diesen drei Punkten (Spitze, Mittelpunk des Basiskreises und Peripheriepunkt unter der Spitze) gebildet wird. Dann musst du nur noch den Winkel zwischen den beiden Seiten des Dreiecks ausrechnen, die sich in der Spitze schneiden und mit 2 multiplizieren.

Habe ich auch gerade gedacht, aber das ist ja nicht der Öffnungswinkel der abgerollten Mantelfläche. Dieser ist um einiges größer.

Meine Berechnung wäre:

Die Wurzel der Summe der Quadrate von Höhe des Kegels und Radius des Basiskreises ist die Gerade vom Mittelpunkt des Kreises zur Spitze. Nach dem Sinussatz habe ich nun einen Winkel von gut 35°. Mit 2 multipliziert komme ich ja auf 70°, aber auch das scheint mit deutlich zu wenig als Öffnungswinkel (Ich denke daran, dass, wenn man die Mantelfläche an der längsten Kante des Kegels aufschneidet, also genau gegenüber der Höhe (Auf einem Punkt der Peripherie des Basiskreises), ja die Außenseiten der Mantelfläche 12 cm (Größte Kantenlänge des Kegels) betragen müssen).

Gruß xgx7

 

[Squart]

Wenn ich etwas Heuristik walten lasse, dann behaupte ich, dass der Mantel deines Kreiskegels ein gleichschenkliges Dreieck mit der Höhe 7 und dem Nicht-Schenkel 2*5*pi ist. Ein Schenkel hat dann die Länge s = Wurzel ((5*pi) hoch 2 + 7 hoch 2). Du willst phi haben, dann ist cos(phi/2) = 7/s => phi = 2* (cos-1(7/s)). Könnte das so stimmen?

@tjp: Danke, du würdest mir einen großen Gefallen tun.
@Cortex85: Ich denke mal, dass Induktion höchstens bei der letzten Behauptung verwendet werden kann. Aber das schaue ich mir morgen an. Danke aber, für deine Hilfe.

Gute Nacht
Squart

 

[xgx7]

Moin xgx7,

ich hoffe ich ahne was du meinst. Abgerollt gleich abgewickelt, spricht so als ob du den Kegel aus einem flachen Blatt Papier basteln möchtest?

Ja, genau so! :-D

2 x 5 x Pi = 31,51 Tatsächlicher Umfang als Kegel
2 x 7 x Pi = 44,12 Gesamtumfang als abgewickelter Kegel

Ich glaube, d. h. ich weiß nichts, da liegt ein Trugschluß. Nämlich der, das der Gesamtumfang des abgewickelten Kegels eben ein ganzer Kreis ist. Es ist nämlich IMVHO (V=Very) ein Kreissektor, mit eben jenem gesuchten Öffnungswinkel.

Die Differenz (12,61) ergibt den äußeren Rand des fehlenden Segments. Das fehlende Segment verhält sich zum Gesamtumfang des flachen Kegels wie der gesuchte Winkel zu 360 Grad. Also 360 / (44,12 / 12,61) = 102,89 Grad. Dies ist der Winkel für das fehlende Segment. Der Rest ist dann eben 360 Grad minus diesem Wert.

Klingt ganz logisch, doch so ganz komme ich noch nicht mit. Ich denke noch...

Nachtrag: Wenn das auch nicht die Frage war, mach doch mal 'ne Zeichnung.

Schon vorher geschehen. Soll ich sie mal hochladen?

 

[KayHH]

Moin xgx7,

Ja, genau so! :-D

Ich glaube, d. h. ich weiß nichts, da liegt ein Trugschluß. Nämlich der, das der Gesamtumfang des abgewickelten Kegels eben ein ganzer Kreis ist. Es ist nämlich IMVHO (V=Very) ein Kreissektor, mit eben jenem gesuchten Öffnungswinkel./

ah, wir haben uns verstanden. Beachte bitte meine vorherigen Nachträge. Du bist auf dem richtigen Weg. Die 2 x 7,43 x Pi = 46,83 sind in der Tat der Gesamtumfang, also quasi imaginär, da eben ein Segment fehlt. Den tatsächlich vorhandenen Umfang hast du ja. Das ist der aus den 5 cm. Die Differenz ist das fehelnde Stück. Dann siehe meinen vorherigen Beitrag. Na …


Gruss KayHH

 

[KayHH]

110,68

 

[xgx7]

Moin xgx7,


ah, wir haben uns verstanden.

Denke ich auch vorerst auch.

Beachte bitte meine vorherigen Nachträge

.
Ah, den zweiten hatte ich noch nicht gesehen.

Du bist auf dem richtigen Weg. Die 2 x 7,43 x Pi = 46,83 sind in der Tat der Gesamtumfang, also quasi imaginär, da eben ein Segment fehlt. Den tatsächlich vorhandenen Umfang hast du ja. Das ist der aus den 5 cm. Die Differenz ist das fehelnde Stück. Dann siehe meinen vorherigen Beitrag. Na ...

Nein, der tatsächliche Umfang ist eben unbekannt. Der aus den 5 cm (2*5*pi) ist nur die Außenseite des Mantels (Und Umfang des Kreises), da diese Seiten ja vor dem Aufschneiden aneinander lagen (Bzw. der Kegel ja auf dem Kreis stand).

Wenn ich etwas Heuristik walten lasse, dann behaupte ich, dass der Mantel deines Kreiskegels ein gleichschenkliges Dreieck mit der Höhe 7 und dem Nicht-Schenkel 2*5*pi ist. Ein Schenkel hat dann die Länge s = Wurzel ((5*pi) hoch 2 + 7 hoch 2). Du willst phi haben, dann ist cos(phi/2) = 7/s => phi = 2* (cos-1(7/s)). Könnte das so stimmen?

Im Prinzip könnte das hinkommen. Ein gleichschenkliges Dreieck ist es auf jeden Fall, nur ist eben 2*5*pi der Umfang des Basiskreises und deshalb Außenseite des abgewickelten Mantels des Kegels. Und der ist rund. Von daher kann man da IMHO kein Dreieck berechnen.

Gruß xgx7

 

[KayHH]

Sorry, es ist schon spät der Radius ist ja 5 cm also musst du mit 8,60 und nicht wie von mir zuvor geschrieben mit 7,43 rechnen. Dafür ist meine Weinflasche gleich leer *aaarrrgghhh*.


Gruss KayHH

 

[xgx7]

Falls du noch da bist:

Wie kommst du auf 8,60 cm ?

Gruß xgx7

 

[KayHH]

Moin xgx7,

so nun habe ich es mal per Hand aufgeschrieben. Ich hoffe du kannst das lesen. Das Foto ist nicht so toll geworden.


Gruss KayHH


Nachtrag: Das in der letzten Zeile soll 360 MINUS 209,26 = 150,75 heißen.

 

[xgx7]

Vielen Vielen dank für die Mühe! :-D


Sorry falls ich nerve, aber ich wills nit nur rechnen sondern auch verstehen. Die Spitze liegt doch oberhalb eines Punktes der Peripherie des Basiskreises.

Von daher sind 7 cm auch die wahre Höhe. Oder ?

Dann würde dein Beitrag Nr. 10 schon stimmen...